Chapter3: Arithmetic for Computer

Addition and Subtraction

先贴一张ALU大致的原理图在这。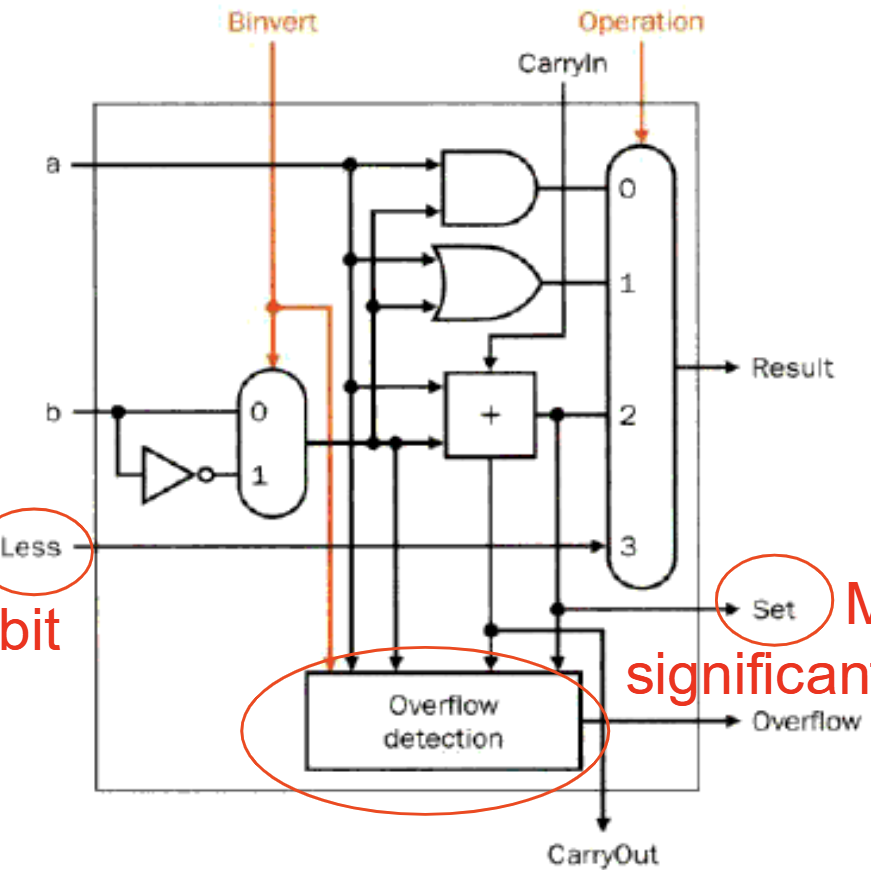

我将根据这张图列出一些需要注意的知识点。

Comparison

这里涉及到较为重要的slt指令，slt(set on less than)，举个例子：

slt rd, rs, rt 对于这条指令，如果rs < rt，那么rd=1，否则rd=0。

Overflow Detection

只需对最高位全加器的低位进位和向高位进位的两个信号做异或，二者信号如果不同则发生了overflow。

Subtraction

减法的拓展非常简单，将B取反并设CarryIn为1即可。

最终的ALU模块如下图所示

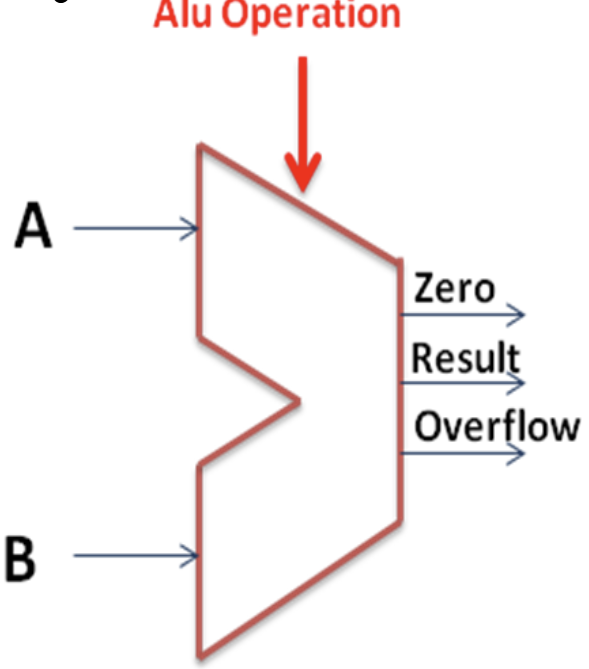
其中的Zero信号表示检测输出结果是否为0，这个信号在后续的某些指令中会用到。

目前我们得到的ALU功能表如下图所示

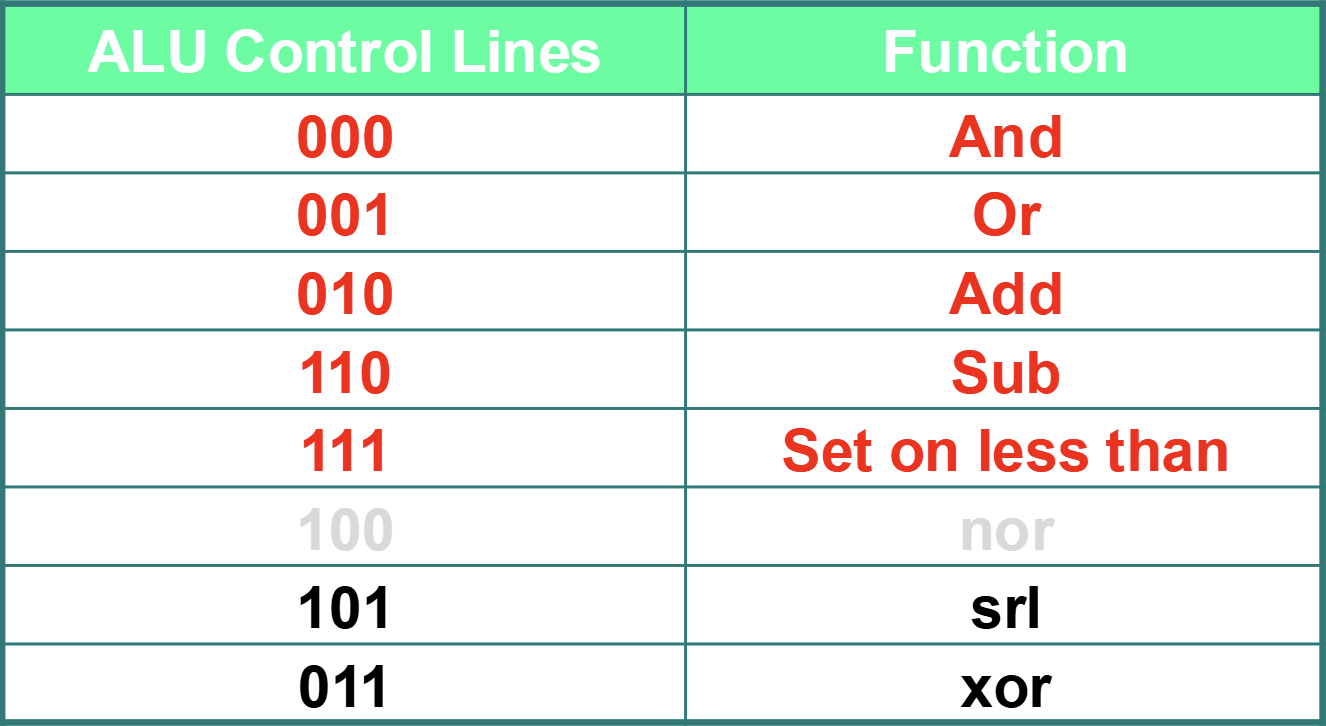
其中的srl为逻辑右移操作。

对于ALU中的加法器还有一些超前进位的优化内容，但已经在计算机逻辑设计基础中学过，此处不再赘述。

Multiplication

实际上计算机做乘法和徒手计算类似，都是把乘数一位一位和被乘数相乘，最后把所有的结果相加即可。

第一代乘法器

它的逻辑原理图如下图所示。

可以看到这种乘法器非常接近徒手计算的操作，也非常容易理解。它的缺点非常明显：占用内存太大，计算太慢。

第二代乘法器

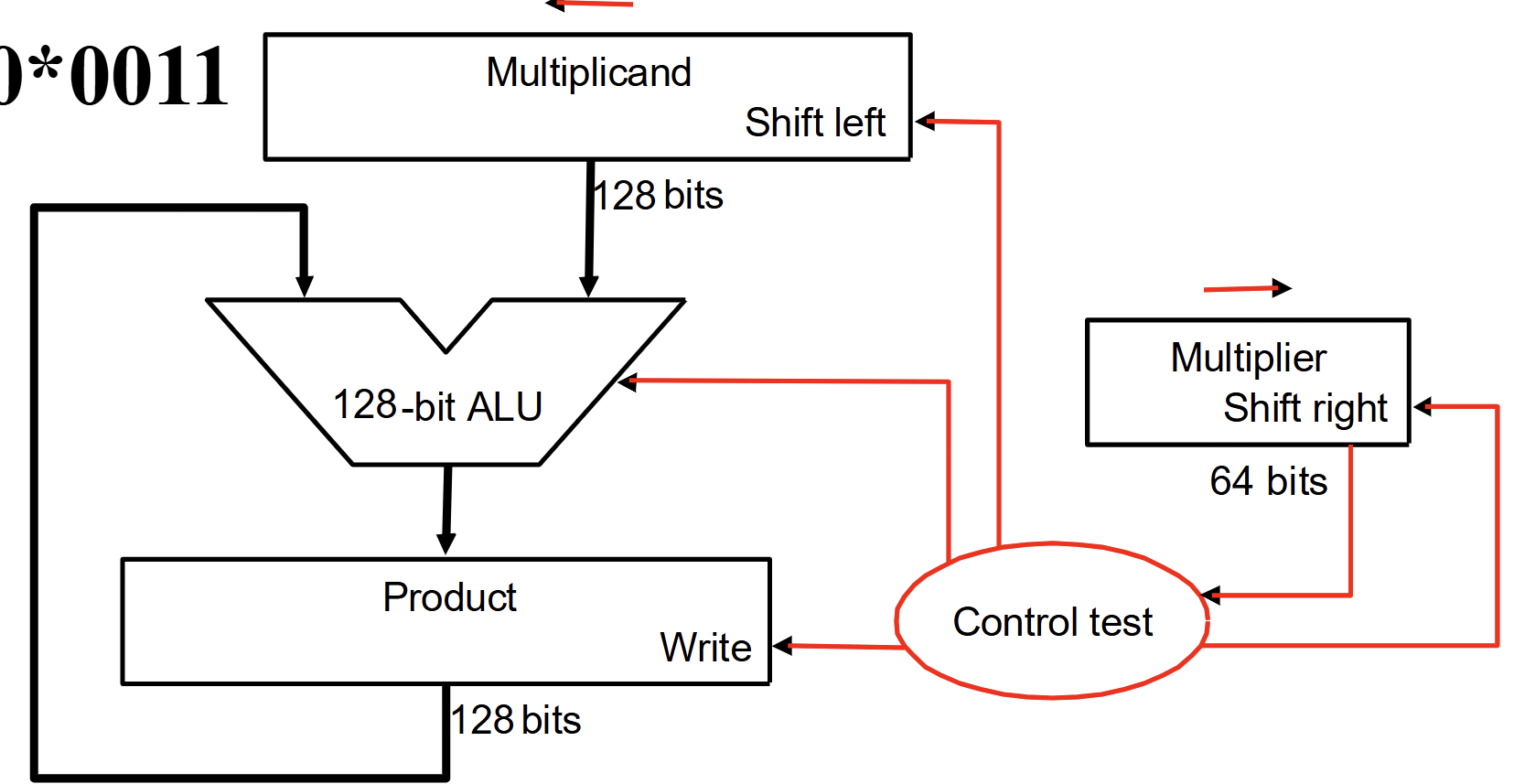
它的逻辑原理图如下图所示。

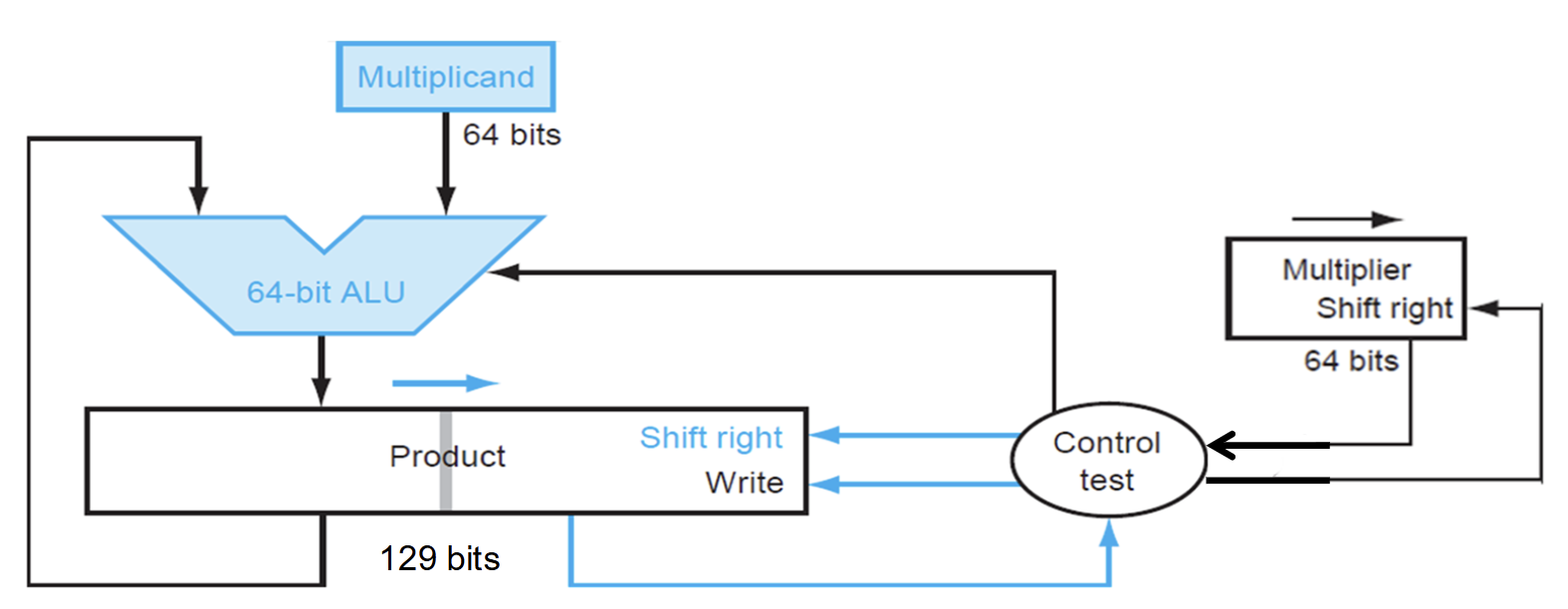
可以看出来它相对于第一代乘法器减少了被乘数所占用的一半内存，并且增加了Product寄存器的右移功能。但是Product寄存器的低64bits好像浪费了，于是就有了第三代乘法器。

第三代乘法器

它的逻辑原理图如下图所示。

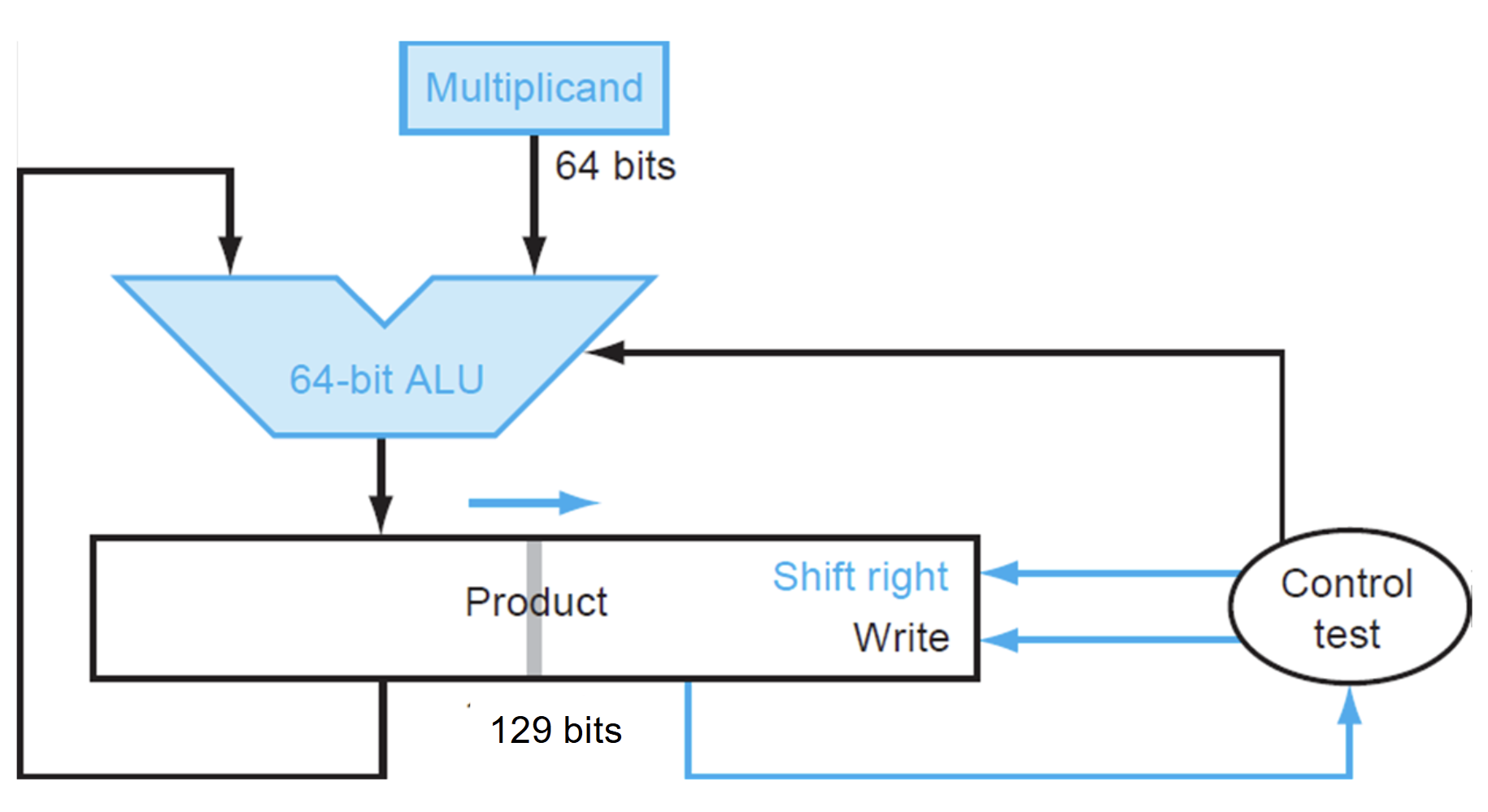
相对于第二代，该乘法器直接把乘数放在Product寄存器的低64bits，这样就节省了乘数的内存占用。

对于Product寄存器为什么增加到129bits: 我正在思考

Booth’s Algorithm

对于乘数中有较多连续出现的1序列，该算法能够大大提高运算速度。

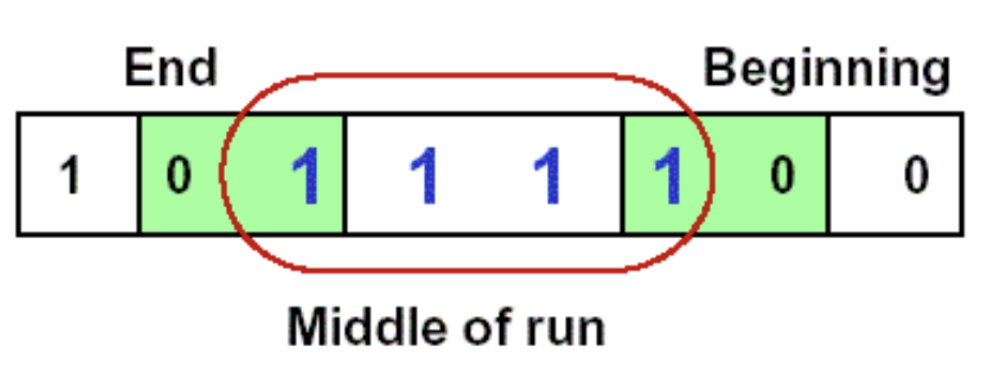
举个ppt上给出的例子：

因此只需要在发生0到1的跳变时减去1位所对应的二进制数，然后跳过后面所有连续接收到的1，最后在发生1到0的跳变时加上0位为1时所对应的二进制数。

Division

有空再补

Floating point numbers

IEEE 754

整个数的值为：

注意bias! 单精度浮点和双精度浮点的bias分别为127和1023。

IEEE754浮点数表示有隐藏1。

Single Precision

单精度浮点数能够表示的范围较小，表示的范围是:

Double Precision

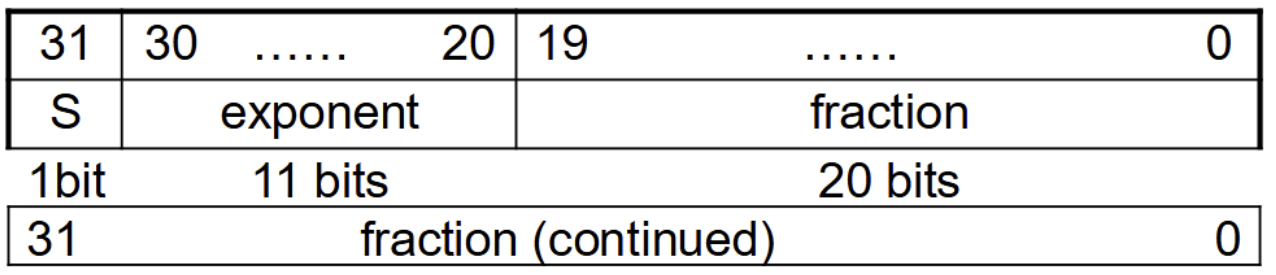
由于所占位数double，双精度浮点数能够表示的范围要远大于单精度浮点数，表示的范围是:

Limitations

Overflow:

The number is too big to be represented.

Underflow:

The number is too small to be represented.

Round method: Round to nearest even.

仅在有效位后一位为1，但之后全零的情况下使用该方法判定，即总是保持LSB为0，如果有效位是1则对有效位进位。